三、等值计算

　　（一）影响资金等值的因素

　　如前所述，由于资金的时间价值，使得金额相同的资金发生在不同时间，会产生不同的价值。反之，不同时点金额不等的资金在时间价值的作用下，却可能具有相等的价值。这些不同时期、不同数额但其“价值等效”的资金称为等值，也称为等效值。

　　影响资金等值的因素有三个：资金的多少、资金发生的时间及利率（或折现率）的大小。

　　（二）等值计算方法

　　常用的资金等值计算主要包括两大类，即：一次支付和等额支付。

　　1. 一次支付的情形

　　（1）终值计算（已知P求F）。现有一笔

　　资金P，年利率为i，按复利计算，则n年末的

　　本利和F为多少？即已知P、i、n，求F.其现金流量如图2.1.2 所示。

　　F＝P（1＋i）n （2.1.8）

　　式中：i 计息周期复利率；

　　n 计息周期数；

　　P 现值（即现在的资金价值或本金，Present Value），指资金发生在（或折算为）某一特定时间序列起点时的价值；

　　F终值（n期末的资金价值或本利和，Future Value），指资金发生在（或折算为）某一特定时间序列终点的价值。

　　式（2.1.8）中的（1＋i）n称为一次支付终值系数，用（F／P，i，n）表示，则式（2.1.8）又可写成：

　　F＝P（F／P，i，n） （2.1.9）

　　[例2.1.4]

　　（2）现值计算（已知F求P）。由式（2.1.8）即可求出现值P.

　　P＝F（1＋i）－n （2.1.10）

　　式中（1＋i）－n称为一次支付现值系数，用符号（P／F，i，n）表示，并按不同的利率i和计息期n列表于附录。在工程经济分析中，一般是将未来时刻的资金价值折算为现在时刻的价值，该过程称为“折现”或“贴现”，其所使用的利率常称为折现率或贴现率。故（1＋i）－n或（P／F，i，n）也可称为折现系数或贴现系数。式（2.1.10）常写成：

　　P＝F（P／F，i，n） （2.1.11）

　　[例2.1.5]

　　等额支付系列情形

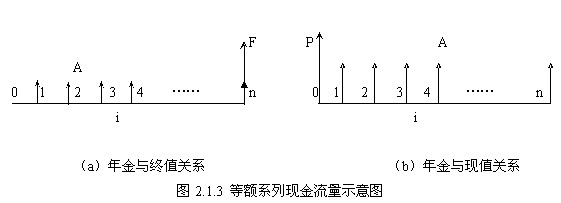
　　A--年金，发生在（或折算为）某一特定时间序列各计息期末（不包括零期）的等额资金序列的价值。

　　对于等额系列现金流量，其复利计算方法如下：

　　（1）终值计算（即已知A求F）。

　　式中称为等额系列终值系数或年金终值系数，用符号（F／A，i，n）表示，式（2.1.16）又可写成：

　　F＝A（F／A，i，n） （2.1.17）

　　[例2.1.6]

　　（4）偿债基金计算（已知F求A）。偿债基金计算是等额系列终值计算的逆运算，故由式（2.1.16）可得：

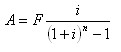
　　式中称为等额系列偿债基金系数，用符号（A／F，i，n）表示，则式（2.1.22）又可写成：

　　A＝F（A／F，i，n） （2.1.23）

　　等额系列偿债基金系数（A／F，i，n）可从附录中查得。

　　[例2.1.9]

　　（2）现值计算（即已知A求P）。由式（2.1.10）和式（2.1.16）得：

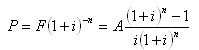
　　式中称为等额系列现值系数或年金现值系数，用符号（P／A，i，n）表示，则式（2.1.18）又可写成：

　　P＝A（P／A，i，n） （2.1.19）

　　[例2.1.7]

　　（3）资金回收计算（已知P求A）。等额系列资金回收计算是等额系列现值计算的逆运算，故由式（2.1.18）可得：

　　式中称为等额系列资金回收系数，用符号（A／P，i，n）表示，则式（2.1.20）又可写成：

　　A＝P（A／P，i，n） （2.1.21）

　　等额系列资金回收系数（A／P，i，n）可从附录中查得。

建设工程教育网整理