咨询方法与实务1——回归分析

2007-03-16 13：33　　来源：　　字体：大小　　打印

　　［背景介绍］

　　某产品过去五年的销售额与目标市场人均收入的数据如下表，预计2006年该产品的目标市场人均收入为1800元。

　　　　　1999-2003历年产品销售额与目标市场人均收入表

　　已知如下数据：1999-2003历年产品销售额的平方和为6 465，1999-2003历年人均收入的平方和为7 652 500，1999-2003历年人均收入与产品销售额乘积之和为222 400.

　　［问题］1.建立一元线性回归模型（小数点后3位）。

　［解答］设该产品销售额为因变量Y，人均收入为自变量X，建立一元回归模型Y=a+bx.由题意，

　　得到一元线性回归模型：Y=5.05+0.025X.

　　［问题］2.进行相关系数检验（取α=0.05，R值小数点后保留3位，相关系数临界值可见附表）。

相关系数临界值表

　　［解答］

　　根据一元线性回归方程，将值代入，求得分别为：30.05、35.05、36.3、37.55、40.05.所以

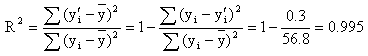
　　得R=0.997

　　查表知α=0.05，自由度=n-2=5-2=3时，得R_0.05=0.878

　　因R=0.997 ＞0.878= R_0.05

　　表明在α=0.05的显著性检验水平上，检验通过，说明人均收入与该产品销售额线性相关的假定是合理的（或者产品销售额和人均收入之间的线性关系成立）。

　　［问题］3.对2006年可能的销售额进行点预测。

　　［解答］已知X₂₀₀₆=1800元，代入模型得Y₂₀₀₆=a+bX₂₀₀₆=5.05+0.025×1800=50.05万元

　　［提示］一元线性回归预测是大纲中要求掌握的内容，复习时要牢记方程式以及其中各个符号代表的含义、回归系数的计算方法。回归检验要能够理解、计算相应的系数R²、t_b、F，必须学会查表（表格一般都会给出）并根据查得的数据解释x和y是否成线性。

　　这是这类题目有点像数学计算题，前后推导关系紧密。考试时，要详细写出计算过程，特别是计算公式和一些符号的含义不能写错，结论也是不能缺少的。

建设工程教育网原创·转载请注明出处

为您推荐

猜你想看

咨询工程师