学员咨询:
1.根据专家调查获得的某产品售价的概率分布如下表:
售价 100元 110元 120元 130元 140元 150元
概率 0.05 0.15 0.25 0.35 0.15 0.05
累计概率 0.05 0.2 0.45 0.8 0.95 1.00
若抽取的随机数为68216,则相对应的售价的抽样值为(126.63元)
2.已知某项目静态投资X服从三角形分布,其中投资的乐观值、最可能值、悲观值分别为x1 x2 x3,且x2=(x1+x3)/2,x4=(x2+x3)/2,x5=(x1+x2)/2,则下面计算正确的是(BCD)
A x≤x4的概率为1/8
B x≤x5的概率为1/8
C x≤x2的概率为1/2
D x5≤x≤x4的概率为3/4
E x5≤x≤x2的概率为1/4
这两题学生一点也摸不着头脑,请老师讲解,谢谢!
教师解答:
1.参见教材204页。根据抽取的随机数,则需要计算累计概率为0.68216所对应的售价,根据所给的售价表,在120元到130元之间,通过线性插值,得对应的售价抽样值=120+(130-120)/0.35*[0.68216-(0.05+0.15+0.25)]=120+2.3216/0.35=126.63元。
2.根据题意,根据三角形分布,其底边上有五个点,在x轴上依次等距排开,分别为1、5、2、4、3,计算概率的时候,分别是计算各部分面积占整个三角形面积的概率即可。参见下图:
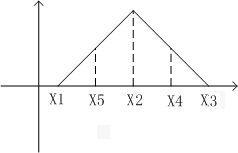
如果把大三角形底和高都当作单位1的话,则对于您说的小于x5的三角形其底和高应该分别为1/4和1/2,那么之比应该为1/8。您看呢?请您静下心来一步一步的认真计算。
建设工程教育网原创·严禁转载






